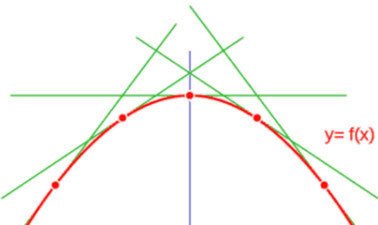
Description
The course “Theory of Real Functions” is proposed for B.Sc. (Hons) Mathematics as the Core course. The course is an indispensable part of pure and applied mathematics which equip the undergraduate students to have a deeper and thorough understanding of the Functions of Real Variables and to apply the concepts of Limits, Continuity and Differentiability in real world problems. The course includes the introduction to Real Functions, Limits, Continuity, Uniform Continuity, Differentiability, Intermediate Value Property, Mean Value Theorems, Taylor’s and Maclaurins’ Series expansions, Riemann integration and Improper integrals. The primary Learning Outcome of this course is Quantitative Reasoning, which is to understand and apply mathematical concepts, analyze and interpret various types and properties of Real Functions. The Learning Outcomes will be assessed through targeted questions - either the comprehensive final or an outside assignment. The applications of mathematics in various disciplines are seeking more analytical skills and deeper understanding of Real Functions. This course enable the students who are interested in Economics, Physics, Engineering and Business Management to develop the skills in analysing and solving different types of functions of real variables which emerge in mathematical modelling of real world problems.
Tags
Syllabus
1 Day 1 Module 1 : Introduction to Real Functions Day 2 Module 2 : Limits: Definition and Properties Day 3 Module 3 : Sequential Criterion for Limits Day 4 Interaction based on the three modules covered Day 5 Assignment
2 Day 1 Module 4 : Limit Theorems: Part I Day 2 Module 5 : Limit Theorems: Part II Day 3 Module 6 : One sided Limits Day 4 Interaction based on the three modules covered Day 5 Assignment
3 Day 1 Module 7 : Infinite limits Day 2 Module 8 : Limits at infinity Day 3 Module 9 : Continuous Functions Day 4 Interaction based on the three modules covered Day 5 Assignment
4 Day 1 Module 10 : Combinations of Continuous Functions Day 2 Module 11 : Composition of Continuous Functions Day 3 Module 12 : Continuous Functions on Intervals, Boundedness theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
5 Day 1 Module 13 : Maximum Minimum Theorem Day 2 Module 14 : Location of Roots Theorem Day 3 Module 15 : Bolzano’s Intermediate Value Theorem Day 4 Day 5 Assignment
6 Day 1 Module 16 : Uniform Continuity Day 2 Module 17 : Lipschitz Function Day 3 Module 18 : Continuous Extension Theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
7 Day 1 Module 19 : Approximations Day 2 Module 20 : Monotone Functions Day 3 Module 21 : Inverse Functions Day 4 Interaction based on the three modules covered Day 5 Assignment
8 Day 1 Module 22 : Differentiability: Introduction to Derivatives Day 2 Module 23: Tangent lines and Rates of Change Day 3 Module 24 : Chain Rule and Caratheodery’s theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
9 Day 1 Module 25 : Derivatives of Inverse Functions Day 2 Module 26 : Role of Derivatives in Real World Day 3 Module 27: Differentials and Linear approximations Day 4 Interaction based on the three modules covered Day 5 Assignment
10 Day 1 Module 28 : Extrema of Functions Day 2 Module 29 : Rolle’s theorem & Mean Value Theorem Day 3 Module 30 : Applications of Mean Value Theorem Day 4 Day 5 Assignment
11 Day 1 Module 31 : Intermediate Value Property, Darboux’s Theorem Day 2 Module 32 : Increasing and Decreasing Functions Day 3 Module 33: L’ Hôpital’s Rule Day 4 Interaction based on the three modules covered Day 5 Assignment
12 Day 1 Module 34 : Concavity and Inflection Points Day 2 Module 35 : Cauchy’s Mean Value Theorem Day 3 Module 36 : Taylor’s theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
13 Day 1 Module 37 : Applications of Taylor’s theorem, Newton’s Method Day 2 Module 38 : Taylor’s Series Day 3 Module 39 : Maclaurin’s Series Day 4 Interaction based on the three modules covered Day 5 Assignment
14 Day 1 Module 40 : Applications of Taylor’s and Maclaurins’ series Day 2 Module 41 : Partitions and Riemann Sums Day 3 Module 42 : Properties of Riemann integrals Day 4 Day 5 Assignment
15 Day 1 Module 43 : Existence of Riemann Integrals Day 2 Module 44 : Riemann Integrable Functions Day 3 Module 45 : Additivity Theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
16 Day 1 Module 46 : Fundamental Theorem of Calculus Day 2 Module 47 : Substitution Theorem Day 3 Module 48 : Improper Integrals Day 4 Interaction based on the three modules covered Day 5 Assignment
17 Day 1 Module 49 : Applications of Improper Integrals Day 2 Module 50 : Cauchy Principal Value and Tests for convergence Day 3 Revision Day 4 Day 5 Assignment

-
TypeOnline Courses
-
ProviderSwayam
1 Day 1 Module 1 : Introduction to Real Functions Day 2 Module 2 : Limits: Definition and Properties Day 3 Module 3 : Sequential Criterion for Limits Day 4 Interaction based on the three modules covered Day 5 Assignment
2 Day 1 Module 4 : Limit Theorems: Part I Day 2 Module 5 : Limit Theorems: Part II Day 3 Module 6 : One sided Limits Day 4 Interaction based on the three modules covered Day 5 Assignment
3 Day 1 Module 7 : Infinite limits Day 2 Module 8 : Limits at infinity Day 3 Module 9 : Continuous Functions Day 4 Interaction based on the three modules covered Day 5 Assignment
4 Day 1 Module 10 : Combinations of Continuous Functions Day 2 Module 11 : Composition of Continuous Functions Day 3 Module 12 : Continuous Functions on Intervals, Boundedness theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
5 Day 1 Module 13 : Maximum Minimum Theorem Day 2 Module 14 : Location of Roots Theorem Day 3 Module 15 : Bolzano’s Intermediate Value Theorem Day 4 Day 5 Assignment
6 Day 1 Module 16 : Uniform Continuity Day 2 Module 17 : Lipschitz Function Day 3 Module 18 : Continuous Extension Theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
7 Day 1 Module 19 : Approximations Day 2 Module 20 : Monotone Functions Day 3 Module 21 : Inverse Functions Day 4 Interaction based on the three modules covered Day 5 Assignment
8 Day 1 Module 22 : Differentiability: Introduction to Derivatives Day 2 Module 23: Tangent lines and Rates of Change Day 3 Module 24 : Chain Rule and Caratheodery’s theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
9 Day 1 Module 25 : Derivatives of Inverse Functions Day 2 Module 26 : Role of Derivatives in Real World Day 3 Module 27: Differentials and Linear approximations Day 4 Interaction based on the three modules covered Day 5 Assignment
10 Day 1 Module 28 : Extrema of Functions Day 2 Module 29 : Rolle’s theorem & Mean Value Theorem Day 3 Module 30 : Applications of Mean Value Theorem Day 4 Day 5 Assignment
11 Day 1 Module 31 : Intermediate Value Property, Darboux’s Theorem Day 2 Module 32 : Increasing and Decreasing Functions Day 3 Module 33: L’ Hôpital’s Rule Day 4 Interaction based on the three modules covered Day 5 Assignment
12 Day 1 Module 34 : Concavity and Inflection Points Day 2 Module 35 : Cauchy’s Mean Value Theorem Day 3 Module 36 : Taylor’s theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
13 Day 1 Module 37 : Applications of Taylor’s theorem, Newton’s Method Day 2 Module 38 : Taylor’s Series Day 3 Module 39 : Maclaurin’s Series Day 4 Interaction based on the three modules covered Day 5 Assignment
14 Day 1 Module 40 : Applications of Taylor’s and Maclaurins’ series Day 2 Module 41 : Partitions and Riemann Sums Day 3 Module 42 : Properties of Riemann integrals Day 4 Day 5 Assignment
15 Day 1 Module 43 : Existence of Riemann Integrals Day 2 Module 44 : Riemann Integrable Functions Day 3 Module 45 : Additivity Theorem Day 4 Interaction based on the three modules covered Day 5 Assignment
16 Day 1 Module 46 : Fundamental Theorem of Calculus Day 2 Module 47 : Substitution Theorem Day 3 Module 48 : Improper Integrals Day 4 Interaction based on the three modules covered Day 5 Assignment
17 Day 1 Module 49 : Applications of Improper Integrals Day 2 Module 50 : Cauchy Principal Value and Tests for convergence Day 3 Revision Day 4 Day 5 Assignment
Tags
Related Courses


Mathemateg bob dydd 2
Introduction to Logic

Fractals and Scaling

Groups: Motion, symmetry and puzzles

Aléatoire : une introduction aux probabilités - Partie 2
Game-Theoretic Solution Concept with Spreadsheets

Metric Spaces and Complex Analysis

AEPA Middle Grades Mathematics (NT203): Practice & Study Guide

Ohio State Test - Mathematics Grade 7: Practice & Study Guide

GACE Paraprofessional Assessment (177) Prep


 Online Courses
Online Courses  Swayam
Swayam
